Translates a number u uniformly distributed between 0 and 1 into a Gaussian distributed one z. More...

#include <FastAndPoorGauss.h>

Public Types
using	Data_t = T
	Type of data to deal with. More...

Public Member Functions

Data_t	transform (Data_t const u) const
	Returns the Gaussian distributed value corresponding to `u`. More...

Data_t	operator() (Data_t const u) const

Static Public Attributes
static constexpr std::size_t	NPoints = N
	Number of sampled points. More...

Private Member Functions
std::size_t	indexOf (Data_t u) const
	Returns the index of the precomputed table serving the value `u`. More...

Static Private Member Functions
static std::array< Data_t, NPoints >	makeSamples ()
	Fills the pre-sampling table. More...

Static Private Attributes
static std::array< Data_t, N > const	fSamples = util::FastAndPoorGauss<N, T>::makeSamples()
	Sampled points of inverse Gaussian. More...

Detailed Description

template<std::size_t N, typename T>
class util::FastAndPoorGauss< N, T >

Translates a number u uniformly distributed between 0 and 1 into a Gaussian distributed one z.

Parameters

N	number of possible values returned; it must be a power of 2
T	(default: `double`) type of number for u and z

The focus of this algorithm is speed, which is paid with some memory and a lot of precision. The algorithm picks one of only N precomputed possible values for each input. The mapping of 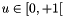$u \in [ 0, +1 [$ into a real number is a multi-step function with N steps. The steps are located at 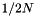$ 1/2N $ steps through the domain of u.

The returned number z is distributed according to a standard normal distribution with mean 0 and standard deviation 1. The number can be turned into one distributed with arbitrary mean 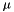$\mu$ and standard deviation 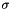$\sigma$ with the usual transformation 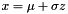$x = \mu + \sigma z$ (see e.g. util::GaussianTransformer).

Resources

Math is internally performed in T precision, except for the initialization that is performed in double precision. The precomputed value table is sizeof(T) * N bytes large.

Note: This class is tuned for performance, and it allocates its data on the stack. Stack overflows have been observed in Linux with a size of N 2^20^. Stack overflows are very puzzling since they do not present any standard diagnostics and debuggers may not notice them. Bottom line is: do not overdo with the number of samples, or ask the author to provide a special version using dynamic memory allocation.

Definition at line 46 of file FastAndPoorGauss.h.

Member Typedef Documentation

template<std::size_t N, typename T>

using util::FastAndPoorGauss< N, T >::Data_t = T

Type of data to deal with.

Definition at line 100 of file FastAndPoorGauss.h.

Member Function Documentation

template<std::size_t N, typename T >

std::size_t util::FastAndPoorGauss< N, T >::indexOf ( Data_t u ) const

private

Returns the index of the precomputed table serving the value u.

Definition at line 234 of file FastAndPoorGauss.h.

                                                             {
   return static_cast<std::size_t>(u * NPoints);
 } // util::FastAndPoorGauss<>::indexOf()

template<std::size_t N, typename T >

auto util::FastAndPoorGauss< N, T >::makeSamples ( )

staticprivate

Fills the pre-sampling table.

Definition at line 241 of file FastAndPoorGauss.h.

 {
   
   std::array<Data_t, NPoints> samples;
   
   double const V2 = std::sqrt(2.0);
   
   util::UniformSequence<Data_t> extract { NPoints };
   
   for(Data_t& value: samples)
     value = static_cast<Data_t>(TMath::ErfInverse(extract() * 2.0 - 1.0) * V2);
   
   return samples;
 } // util::FastAndPoorGauss<>::makeSamples()